
EulerLagrange equations, transvers ality conditions, and necessary optimality conditions for isoperimetric problems, on an arbitrary time scale, are proved. First developed by Euler to determine the shortest paths between fixed. I can see that (maybe a little hand-wavingly) this corresponds to a multiplication by $\text d\alpha/\text d\alpha$, but I'm not sure if that's a valid way to think of it. We develop the calculus of variations on time scales for a functional that is the composition of a certain scalar function with the delta and nabla integrals of a vector valued eld. The calculus of variations is an important tool that is used all over modern physics. $$\delta y\equiv \left(\frac\right)\text d\alpha.$$

However, there is a step in which the $\delta$ notation is defined:

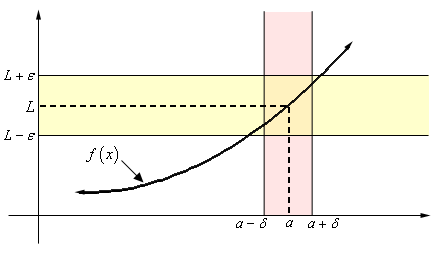
This is extremely useful because computations involving a diagonalizable matrix can often be reduced to much. In Goldstein's classical mechanics (page 36) he introduces the basics of the calculus of variation and uses it to effectively the Euler-Lagrange equations. In mathematics, particularly linear algebra and functional analysis, a spectral theorem is a result about when a linear operator or matrix can be diagonalized (that is, represented as a diagonal matrix in some basis). identifying that the detected delta changes between the different clients. I agree very strongly, there are so many bad treatments of the calculus of variations, despite it often being the very first chapter in Lagrangian mechanics texts.


 0 kommentar(er)
0 kommentar(er)
